군집화 (70%)
군집화란 머신러닝 기법 중 하나로 데이터셋들을 특정 기준으로 묶어 여러개의 군집(Cluster)로 만드는 방법을 의미 합니다. 여기서 기준은 거리, 색상, Feature들이 사용 될 수 있습니다.
PCL에서는 탐지 하려고 하는 물체가 충분히 멀리 떨어져 각 물체 별로 점이 모여 있다는 점을 활용하여 군집화 기반 Segmentation을 수행 합니다.
군집화 방법들은 아래와 같이 분류 할 수 있습니다.
중심 기반 군집화 : 클러스터를 클러스터 중심점으로 정의하는 기법 (eg. Euclidean clustering)
계측적 군집화 : 클러스터의 크기에 따라 클러스터의 계층을 정의하고 계층의 상하위를 이용하는 기법
밀도 기반 군집화 : 클러스터를 데이터가 높은 밀도로 모여 있는 공간으로 보는 기법 (eg. DBSCAN)
본 챕터에서는 PCL에서 제공하는 중심기반 군집화 기법인 Euclidean clustering과 Sklearn에서 제공하는 밀도 기반 군집화 기법인 DBSCAN에 대하여 살펴 보겠습니다.
1. Euclidean clustering
가장 간단한 방법의 군집화 방법으로 두 점사이의 거리를 계산 해서 특정 거리 이하일경우 동일한 군집으로 간주 하는 방법입니다. 이때 거리를 계산 하는 방법으로 Eudclidean Distance를 이용하는 방식을 Euclidean clustering 라고 합니다.
2. DBSCAN
포인트 클라우드 간의 밀도 정보를 이용하여 군집을 구분 하는 방법 입니다. 점이 세밀하게 몰려 있어서 밀도가 높은 부분을 클러스터링 하는 방식이다. 쉽게 설명하면, 어느점을 기준으로 반경 x내에 점이 n개 이상 있으면 하나의 군집으로 인식하는 방식이다.
장점
K Means와 같이 클러스터의 수를 정하지 않아도 됨
클러스터의 밀도에 따라서 클러스터를 서로 연결하기 때문에 기하학적인 모양을 갖는 군집도 잘 찾을 수 있음
단점
많은 연산을 수행하기에 K 평균에 비해 그 속도가 느림
반지름과 임계치 설정에 많은 영향을 받는다
그리고, 유클리드 제곱거리를 사용하는 모든 데이터 모델의 공통적인 단점인, 'Curse Of dimensionality 또한 존재
이는 2차원이나 3차원 등 차원수가 낮은 데이터세트에는 문제가 되지 않지만,
고차원 데이터세트로 갈수록 필요한 학습 데이터 양이 급증하는 문제점이며, 이 때문에 많은 연산이 필요해진다는 단점이 있다.
예 : minPts = 4, 반경 = epsilon
A low minPts means it will build more clusters from noise, so don't choose it too small. How can I choose eps and minPts (two parameters for DBSCAN algorithm) for efficient results?
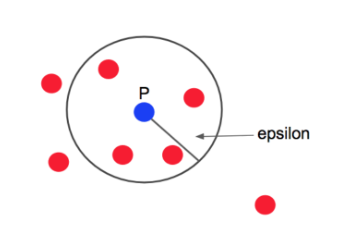
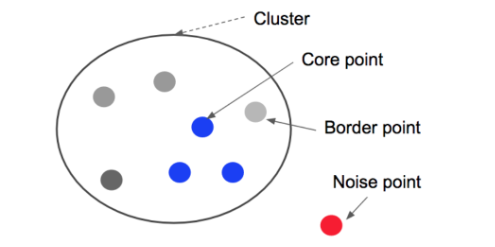
p=코어포인트 . 반경안에 점 4개 존재
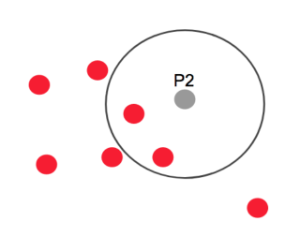
P2=경계점(Border point) . 반경안에 점 4개 없음 . But, Core point에는 속함
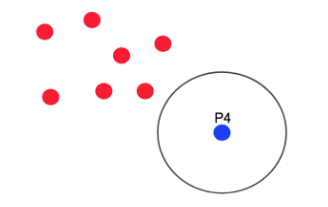
P4=Noise Point . 반경안에 점 4개 없음 .And, Core point에 속하지 않음 (어느군집에도 안속함)
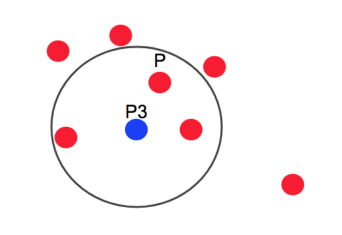
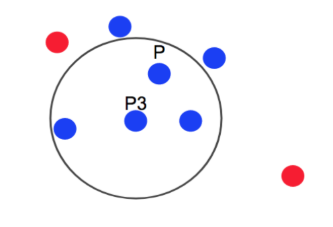
P=코어포인트 P3 = 코어포인트
두 코어 포인트를 연결하여 하나의 군집으로 처리
정리
Last updated
Was this helpful?